The Goldman Equation
It is useful to be able to calculate the membrane potential of a cell when some, or all, of the ions are not in equilibrium. The most commonly used approach is the Goldman equation.
The Goldman equation describes the relationship between the membrane potential (Vm), ion permeabilities and ion concentrations for the membrane permeant ions.
The Goldman equation in its most general form for monovalent cations (C) and anions (A) is,
\[V_{m} = \frac{\text{RT}}{F}\ln{\frac{{\sum_{i}^{n}P_{C_{i}^{+}}\left\lbrack C_{i}^{+} \right\rbrack}_{\text{out}} + {\sum_{j}^{m}P_{A_{j}^{-}}\left\lbrack A_{j}^{-} \right\rbrack}_{\text{in}}}{{\sum_{i}^{n}P_{C_{i}^{+}}\left\lbrack C_{i}^{+} \right\rbrack}_{\text{in}} + {\sum_{j}^{m}P_{A_{j}^{-}}\left\lbrack A_{j}^{-} \right\rbrack}_{\text{out}}}\text{ }}\]
where, \(V_{m}\) is the resting membrane potential, \(P_{C_{i}^{+}}\) is the permeability to the i-th cation and \(P_{A_{j}^{-}}\) is the permeability to the j-th anion. In this form the Goldman equation can take account of an arbitrary number of different ion selective transport systems that may contribute to setting the membrane potential.
The ion permeability of the membrane and the ion conductance are related but they are not identical. Both the permeability of a membrane and the conductance are determined by the number and types of ion channels found in the membrane. Permeability is only dependent on the properties of the membrane and is not dependent on the number of ions in solution. There could be zero ions and the membrane permeability would be unchanged. It is a measure of the ease with which ions flow across a membrane not the rate of flow. In contrast conductance is also dependent on the ion concentration. Conductance is proportional to the rate of flow of ions through a membrane and is determined from Ohm’s Law.
Typically, the three main ions that affect the membrane potential are potassium, sodium and chloride ions. As described previously, there are ion channels that are selective for K+ ions, Na+ ions and Cl- ions. The relative permeabilities of the resting cell membrane for these different ions depends on the channels that are normally open at rest, the so-called leak channels. In a typical cell these leak channels are predominantly K+ ion selective but the membrane also has a small, but non-negligible, Na+ ion permeability.
For this reason, the Goldman equation, at normal body temperature (37°C), is typically simplified to,
\[V_{m} = 61.5\log{\frac{{P_{K}\left\lbrack K^{+} \right\rbrack}_{\text{out}} + P_{\mathit{Na}}\left\lbrack Na^{+} \right\rbrack_{\text{out}}}{P_{K}\left\lbrack K^{+} \right\rbrack_{\text{in}} + {P_{\mathit{Na}}\left\lbrack Na^{+} \right\rbrack}_{\text{in}}}\text{ }}\]
where, \(P_{K}\) is the permeability to K+ ions, and \(P_{\mathit{Na}}\) is the permeability to Na+ ions. The contribution of chloride ions in many cells, not all, is negligible.
The equation is commonly reformulated in terms of relative permeabilities because it is easier to measure relative permeabilities than absolute permeabilities,
\[V_{m} = 61.5\log{\frac{\left\lbrack K^{+} \right\rbrack_{\text{out}} + b\left\lbrack Na^{+} \right\rbrack_{\text{out}}}{\left\lbrack K^{+} \right\rbrack_{\text{in}} + {b\left\lbrack Na^{+} \right\rbrack}_{\text{in}}}\text{ mV}}\]
where, \(b = P_{\mathit{Na}}/P_{K}\), the relative permeability of the membrane to sodium and potassium ions.
Numerical Example
Calculate the membrane potential of a typical nerve cell, using the ion concentrations in Table 1. The ratio of sodium to potassium permeability (\(b\)) is approximately 0.03, i.e. the membrane is approximately 33 times more permeable to K+ ions than to Na+ ions
Table 1. Intracellular and Extracellular Ion Concentrations
| Ion | Intracellular (mM) | Extracellular (mM) |
|---|---|---|
| Na+ | 15 | 140 |
| K+ | 130 | 4.5 |
Substituting these values into the Goldman equation,
\[\begin{aligned}V_{m} &= 61.5\log{\frac{4.5 + 0.03 \times 140}{130 + 0.03 \times 15}\text{\ \ \ mV}}\\\\[-2ex] &= \, - 72\text{ mV}\end{aligned}\]
Measure Relative Permeability
It is possible to determine the relative permeability of the membrane to potassium and sodium ions experimentally by measuring the membrane potential and changing the external potassium concentration \(\left\lbrack K^{+} \right\rbrack_{\text{out}}\). In Figure 1, the dots represent the measured membrane potential at different potassium concentrations. In this particular cell the relative permeability \((b = P_{\mathit{Na}}/P_{K})\) is approximately 0.03.
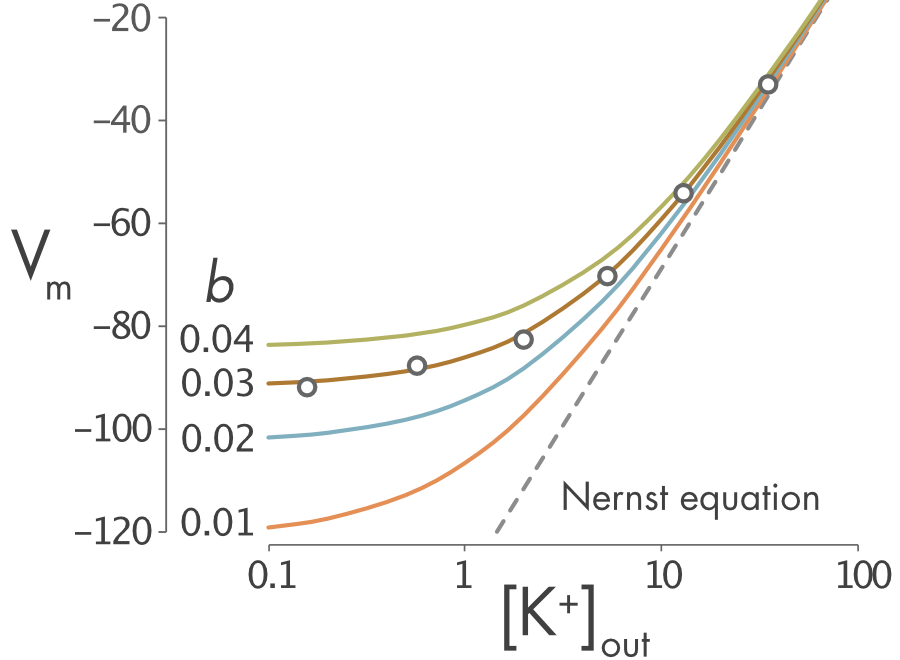
Figure 1 Relationship between external potassium concentration and membrane potential. The Goldman equation has been plotted for different relative permeabilities (0.1 – 0.4). Experimental measurements of resting membrane potential different potassium concentrations are represented by circles. The Nernst equation for potassium ions, which assumes zero permeability to sodium ions, is also plotted (dashed line). It is a straight line on this log plot of potassium concentrations.