Equilibrium Potential
We begin again with a spherical cell with different concentrations of ion X inside and outside the cell (Figure 1). The membrane is permeable only to ion X.
At first the system is not in equilibrium, since there is a large chemical potential difference for ion X. How it achieves equilibrium is quite interesting. As ions flow out of the cell the electric potential difference (\(V_{\text{in}} - V_{\text{out}})\) increases until it is equal and opposite to the chemical potential difference.
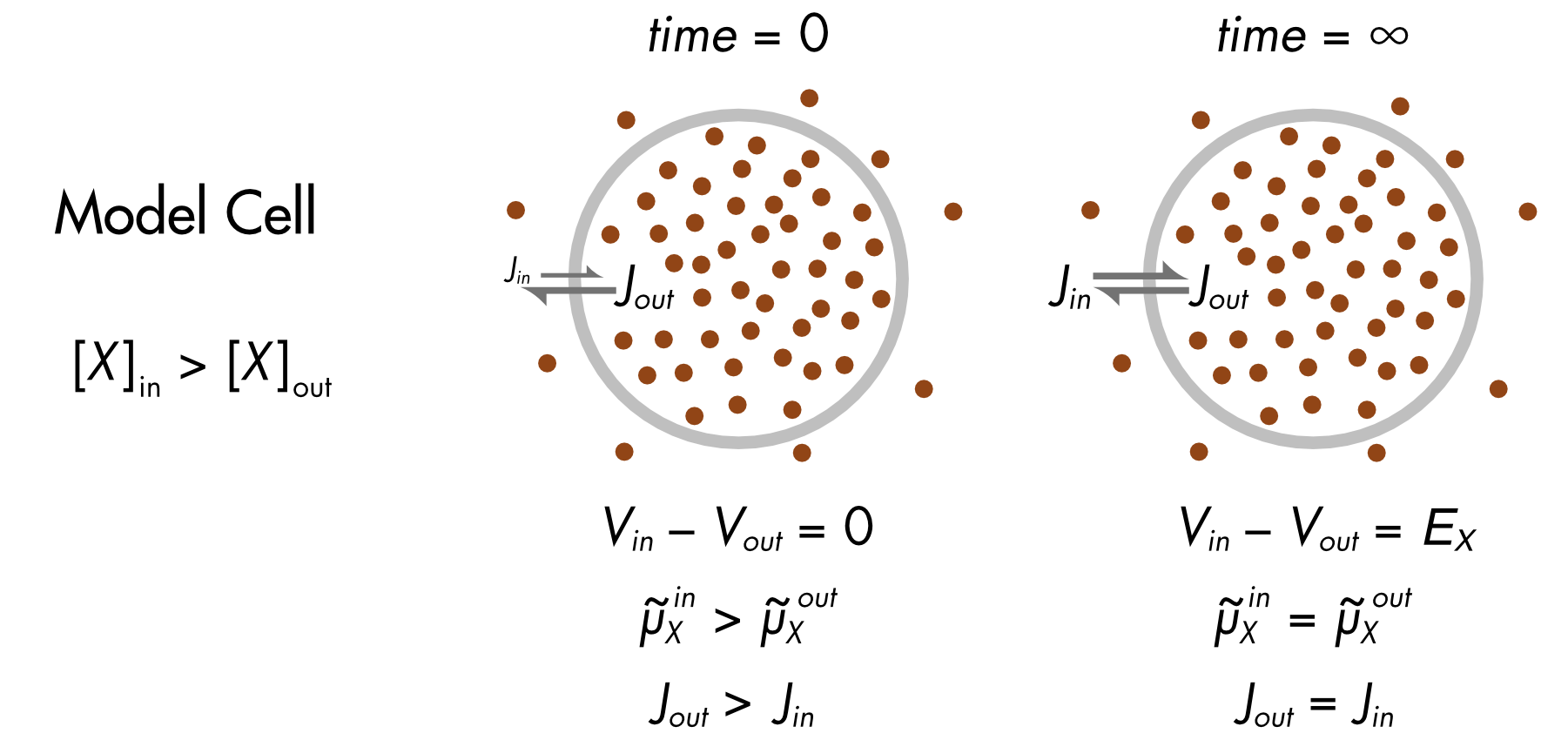
Figure 1 The intracellular and extracellular fluid are aqueous solutions containing ion X and an equal concentration of a counterion (not shown), which has the opposite charge to ion X. The membrane is permeable only to ion X. At time zero the voltage across the cell membrane is zero. At equilibrium the voltage across the membrane is known as the equilibrium potential (EX). It is assumed that there is no significant change in the ion concentrations inside or outside the cell as it evolves towards equilibrium.
Initially (time = 0) the electric potential across the membrane is zero (\(V_{\text{in}} - V_{\text{out}} = 0)\) and the electrochemical potential of the ions inside the cell is greater than outside the cell \(({\widetilde{\mu}}_{X}^{\text{\ in}} > {\widetilde{\mu}}_{X}^{\text{\ out}})\). As a consequence, the outward flux of ion X \({(J}_{\text{out}})\) is larger than the inward flux \({(J}_{\text{in}})\). The resultant net flux of charged ions out of the cell leads to an increasing difference in electrical potential between the inside and outside of the cell that will, at equilibrium, balance the chemical potential difference.
At equilibrium (time = ∞), the electric potential difference equals the chemical potential difference and the electrochemical potentials for ion X inside and outside the cell are equal \(({\widetilde{\mu}}_{X}^{\text{\ in}} = {\widetilde{\mu}}_{X}^{\text{\ out}})\). The one-way fluxes are equal and opposite (\(J_{\text{out}} = J_{\text{in}}\)). The electrical potential across the membrane at this point is known as the equilibrium potential \({(E_{X} = V}_{\text{in}} - V_{\text{out}})\). This value can be calculated using the Nernst equation.
The Nernst Equation
The sum of the chemical potential difference and the electric potential difference for ion X will be zero at equilibrium,
\[\begin{aligned}\Delta\text{chemical\ potential+}\Delta\text{electric\ potential} &= 0\\\\[-2ex] \Delta\mu_{X} + \Delta\phi_{X} &= \ 0\end{aligned}\]
Substituting the equations described previously for both these quantities,
\[\text{RT}\ln{\frac{\left\lbrack X \right\rbrack_{\text{in}}}{\left\lbrack X \right\rbrack_{\text{out}}} + z\text{F}\left( V_{\text{in}} - V_{\text{out}} \right) = 0}\ \]
Rearranging,
\[\text{-RT}\ln{\frac{\left\lbrack X \right\rbrack_{\text{out}}}{\left\lbrack X \right\rbrack_{\text{in}}} + z\text{F}\left( V_{\text{in}} - V_{\text{out}} \right) = 0}\ \]
\[z\text{F}\left( V_{\text{in}} - V_{\text{out}} \right) = \text{RT\ ln}\frac{\left\lbrack X \right\rbrack_{\text{out}}}{\left\lbrack X \right\rbrack_{\text{in}}}\ \]
Substituting \({E_{X} = (V}_{\text{in}} - V_{\text{out}})\),
\[z\text{F}E_{X} = \text{RT\ ln}\frac{\left\lbrack X \right\rbrack_{\text{out}}}{\left\lbrack X \right\rbrack_{\text{in}}}\ \]
Solving for \(E_{X}\) gives the Nernst equation,
\[ E_{X} = \frac{\text{RT}}{z\text{F}}\ln\frac{\left\lbrack X \right\rbrack_{\text{out}}}{\left\lbrack X \right\rbrack_{\text{in}}}\ \ \ \ \ \tag{1} \]
Note that the equilibrium potential is equal and opposite to the chemical potential when it is expressed in the units of volts rather than joules per mole.
\[E_{X} = \frac{{- \Delta\mu}_{X}}{\text{zF}}\]
where F is the Faraday constant, which converts the chemical potential difference from the units of joule per mole, to volts (or joule per coulomb).
The Nernst equation is often simplified, by evaluating RT/F at normal body temperature (37°) and using logarithm to the base 10,
\[E_{X} = \frac{61.5}{z}\log\frac{\left\lbrack X \right\rbrack_{\text{out}}}{\left\lbrack X \right\rbrack_{\text{in}}}\text{\ \ \ }\left( \text{mV} \right)\]
where, \(E_{X}\) is the equilibrium potential of ion X, \(z\) is the valence of the ion (+1 for Na+ and K+, -1 for Cl-), log is the logarithm to the base 10, \(\left\lbrack X \right\rbrack_{\text{out}}\) is the ion concentration outside the cell, and \(\left\lbrack X \right\rbrack_{\text{in}}\) is the ion concentration inside the cell. The units are millivolt (mV).
Microscopic Ion Movement
To understand how the model cell achieves equilibrium it is helpful to consider what happens microscopically, at the level of individual ions (Figure 2). In this animation there is a high concentration of potassium ions inside the cell, equivalent to ion X in the model above, and similar to real cells. There are equal concentrations of anions and cations in both the intracellular and extracellular solutions so that neither solution has a net charge. The membrane is permeant only to potassium ions.
Figure 2 The animation shows a small region of the cell membrane with two potassium channels. There is a higher concentration of potassium and chloride ions inside the cell than outside. There is a large chemical potential difference for potassium ions across the membrane whereas the electric potential difference is initially zero (shown in graph at top). When the potassium channels open, a relatively small number of potassium ions move out of the cell, down their concentration gradient. This creates an excess of positively charged ions outside the cell and an equivalent excess of negatively charged ions inside the cell. As each potassium ion flows out of the cell the electric potential difference increases. This process continues until the electric potential difference equals the chemical potential difference in magnitude. At this point the system is at equilibrium. The one-way fluxes, the flux of potassium ions into and out of the cell, are equal in magnitude and there is no net flux of potassium ions across the membrane.
Once the potassium channels open and the membrane becomes permeable to potassium ions, a relatively small number of potassium ions flow out of the cell, producing an excess of positive charges outside the cell and an excess of negative charges inside the cell. This separation of charge creates the electric potential difference across the membrane that ultimately balances the chemical potential difference and brings the system into equilibrium.
The lipid bilayer allows the ions to interact across the membrane like a capacitor. As a consequence, the excess positive and negative ions on either side of the membrane are not distributed equally throughout the intracellular and extracellular solutions. Because they can interact electrostatically with each other across the bilayer they are drawn towards each other resulting in a sheet of negative ions inside the cell close to the membrane and a sheet of positive ions on the other side of the membrane (Figure 2).
The system is in equilibrium when there is no net movement of ions between the two compartments. The system is not, however, static at the microscopic level. The water and solute molecules continue in endless movement along chaotic trajectories and are constantly exchanging energy as they collide. As a consequence, there are still one-way fluxes across the membrane in both directions, but these fluxes are opposite and equal in magnitude so that the net flux is zero.
Equilibrium Potentials in a Real Cell
The membrane of a typical cell is predominantly permeable to potassium ions but not perfectly permeable, so the membrane potential does not exactly equal the equilibrium potential for potassium ions. This can be demonstrated by calculating the equilibrium potential for each major ion using realistic values for their internal and external ion concentrations (Table 1).
Table 1. Intracellular and Extracellular Ion Concentrations
| Ion | Intracellular (mM) | Extracellular (mM) |
|---|---|---|
| Na+ | 15 | 140 |
| K+ | 130 | 4.5 |
| Cl- | 7 | 116 |
ENa = 61.5 log ([Na+]o / [Na+]i) = 61.5 log(140/15) = +60 mV
EK = 61.5 log ([K+]o / [K+]i) = 61.5 log(4.5/130) = \(-\)90 mV
ECl = \(-\)61.5 log ([Cl-]o / [Cl-]i) = \(-\)61.5 log(116/7) = \(-\)75 mV
Since a typical resting membrane potential in a neuron is close to ‑70 mV, none of the ions are at equilibrium. The cell membrane is not perfectly selective for K+ ions and other ions can also cross the membrane and contribute to setting the membrane potential. While the Nernst equation does not tell the whole story about the membrane potential in real cells it is a useful tool for describing the thermodynamic state of the different ion species.
As in the model cell, separation of charge due to ion fluxes in or out of the cell establishes the membrane potential in real cells.
Ion Flux Required to Generate the Equilibrium Potential
It might be objected that an assumption of the Nernst potential derivation given above, that the concentration of ions inside and outside the cell remain unchanged, is obviously violated, since some ions clearly move from one compartment to another. This effect is exaggerated in Figure 2. On this scale the cell is vastly large and the bulk of the solution inside the cell is unaffected by these relatively small fluxes across the membrane. Nonetheless, it is worthwhile calculating the extent of the changes in order to convince the skeptical student.
The volume of a 50 µm diameter cell is given by,
\[\begin{aligned}\text{volume} &= 4\text{/}3\pi r^{3}\\\\[-2ex] &= 65,450\,\text{μ}\text{m}^{\text{3}}\end{aligned}\]
The concentration of potassium ions inside the cell is 130 mM. Using Avogadro’s number (N = 6.022 × 1023 ions⋅mol-1), the number of potassium ions per unit volume is 7.83 × 107 ions\(\cdot\)µm-3. The number of ions inside the cell can then be calculated,
\[\begin{aligned}\text{number of }\text{K}^{\text{+}}\text{ ions in cell} &= 65,450 \times 7.83 \times 10^{7}\\\\[-2ex] &= 5.12 \times 10^{12}\end{aligned}\]
To calculate the number of charges that must cross the membrane to reach EK first calculate the membrane capacitance (Cm). The surface area of the cell membrane is given by,
\[\begin{aligned}\text{area} &= 4\pi r^{2}\,\\\\[-2ex] &= 7,854\ \text{μ}\text{m}^{\text{2}}\end{aligned}\]
Calculation of the number of ions that must move takes advantage of the known electrical properties of the cell membrane. The specific capacitance of the membrane is approximately 0.01 pF⋅µm-2. The capacitance of our 50 µm diameter cell is calculated by multiplying the membrane area with the specific capacitance,
\[\begin{aligned}C_{m} &= 7,854 \times 0.01\\\\[-2ex] &= 79\,\text{pF}\end{aligned}\]
To calculate the number of ions that must flow into the cell to reach EK, we can take advantage of the fact that this flux of ions must be sufficient to charge the membrane capacitance to EK. Using the definition of capacitance,
\[C = \frac{q}{V}\]
where, C is the capacitance of the membrane, q is the charge held by the capacitor (coulombs), and V is the voltage, which in this case will be the equilibrium potential (EK = −90 mV).
\[\begin{aligned}q &= CV\\\\[-2ex] &= 79 \times 0.09\\\\[-2ex] &= 7.07 \times 10^{- 12}\,\text{coulombs}\end{aligned}\]
Since there are 6.2 × 1018 charges per coulomb, the number of potassium ions that leave the cell is,
\[\begin{aligned}\text{number of }\text{K}^{\text{+}}\text{ ions} &= 7.07 \times 10^{- 12} \times 6.2 \times 10^{18}\,\\\\[-2ex] &= 43.8 \times 10^{6}\end{aligned}\]
The 43.8 million ions that leave the cell in order to establish the equilibrium potential is a large number, but it is small compared to the 5.12 trillion ions in the cell. For a 50 µm cell, one ion leaves for every 117,000 ions that remain. This suggests that the original assumption of no significant change in ion concentration is a reasonable one. This ratio does depend on the size of the cell, as the cell gets smaller the surface to volume ratio increases. However, even for a relatively small 10 µm diameter cell, one ion leaves for every 23,000 ions that remain.
While fluxes of potassium, sodium and chloride ions do not generally result in significant changes in ion concentrations in the cell, this is not true for calcium ions. The concentration of calcium ions inside the cell is so low that even relatively small fluxes can produce significant changes in calcium ion concentration, which is the basis for calcium signaling. Also, potassium ion fluxes out of electrically active cells can have an effect on the external concentration of potassium ions when the cells are in very tightly packed spaces with small volumes of extracellular fluid, which is not uncommon in the nervous system.