Electrochemical Potential
Ion flux across the membrane is a more complex problem than the movement of uncharged solutes because the movement of an ion, which carries a charge, is also affected by any electric potential across the membrane in addition to the chemical potential.
We begin again with a spherical cell but now the solute is an ion with an intrinsic charge (z) and the interior of the cell has a negative electric potential (-70 mV) relative to outside the cell (Figure 1).
Figure 1 Model cell. The intracellular and extracellular fluid is an aqueous solution containing ion X. The two compartments are separated by a membrane that is permeable only to these ions. The electric potential inside of the cell is negative with respect to outside the cell.
As described previously, the difference in chemical potential is given by,
\[\Delta\mu_{\,} = \text{RT}\ln\frac{\left\lbrack X \right\rbrack_{\text{in}}}{\left\lbrack X \right\rbrack_{\text{out}}}\]
The difference in electric potential is given by,
\[\Delta\phi = z\text{F}\,\left( V_{\text{in}} - V_{\text{out}} \right)\]
where, z is the valence of the ion, and F is the Faraday constant.
The electric potential difference \({(V}_{\text{in}} - V_{\text{out}})\) is simply the difference in electrical potential between the inside and outside of the cell. It is typically expressed in the units of volts (V). The chemical potential energy is expressed in joule per mole (J⋅mol-1). In order to match the units of the chemical potential the electric potential is multiplied by the Faraday constant (F), which converts the units from volts (or joule per coulomb) to joule per mole. The valence (z) takes account of whether ion X is positively or negatively charged, and the magnitude of the charge.
The difference in the electrochemical potential between the inside and outside of the cell is given by,
\[\begin{aligned}\Delta\text{electrochemical\ potential} &= \Delta\text{chemical\ potential} + \Delta\text{electric\ potential}\\\\[-2ex] \Delta{\widetilde{\mu}}_{\ } &= \ {\Delta\mu}_{\ } + \text{\ Δ}\phi_{\ }\end{aligned}\]
For ion X,
\[\begin{aligned}\Delta{\widetilde{\mu}}_{X} &= \text{RT}\text{ ln}\frac{\left\lbrack X \right\rbrack_{\text{in}}}{\left\lbrack X \right\rbrack_{\text{out}}} + z\text{F}\left( V_{\text{in}} - V_{\text{out}} \right)\\\\[-2ex] &= \text{RT}\text{ ln}\frac{\left\lbrack X \right\rbrack_{\text{in}}}{\left\lbrack X \right\rbrack_{\text{out}}} + z\text{F}V_{m}\end{aligned}\]
where, \(\Delta{\widetilde{\mu}}_{X}\) is the difference in electrochemical potential (J⋅mol-1), and \({V_{m} = (V}_{\text{in}} - V_{\text{out}})\) is the membrane potential.
Numerical Example
Compare the electrochemical potential of two ions Na+ and K+ when the ion concentrations inside and outside the cell are given in Table 1 and the membrane potential is fixed at Vm = ‑70 mV.
Table 1. Intracellular and Extracellular Ion Concentrations
| Ion | Intracellular (mM) | Extracellular (mM) |
|---|---|---|
| K+ | 130 | 4.5 |
| Na+ | 15 | 140 |
For K+ ions,
\[\begin{aligned}\Delta{\widetilde{\mu}}_{K} &= \text{RT}\ln\frac{130}{4.5} + z\text{F}V_{m}\\\\[-2ex] &= 8.31447 \times 310.15 \times \ln\frac{130}{4.5} + 1 \times 96,485 \times - 0.07\\\\[-2ex] &= 8,673 - 6,754\,\,\text{J}\text{⋅}\text{mo}\text{l}^{\text{-1}}\\\\[-2ex] &= 1.9\,\,\text{kJ}\text{⋅}\text{mo}\text{l}^{\text{-1}}\end{aligned}\]
For Na+ ions,
\[\begin{aligned}\Delta{\widetilde{\mu}}_{\mathit{Na}} &= \text{RT}\ln\frac{15}{140} + z\text{F}V_{m}\\\\[-2ex] &= 8.31447 \times 310.15 \times \ \ln\frac{15}{140} + 1 \times 96,485 \times - 0.07\\\\[-2ex] &= - 5,760 - 6,754\,\,\text{J}\text{⋅}\text{mo}\text{l}^{\text{-1}}\text{\ \ }\\\\[-2ex] &= - 12.5\,\,\text{kJ}\text{⋅}\text{mo}\text{l}^{\text{-1}}\end{aligned}\]
The electrochemical potential difference was defined as the potential inside the cell relative to outside. For potassium ions the net electrochemical potential is positive (1.9 kJ⋅mol-1), which favors the net movement of potassium ions out of the cell (Figure 2). The chemical potential difference and electric potential difference have opposite signs and the chemical potential is larger when the membrane potential equals -70 mV.
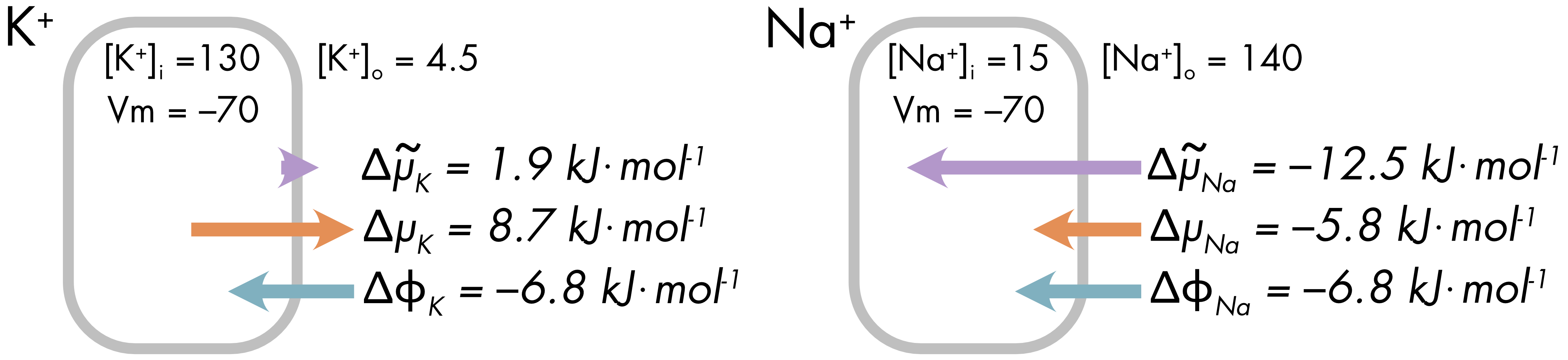
Figure 2 Difference in electrochemical (\(\Delta{\widetilde{\mu}}_{\ }\)), chemical (\(\Delta\mu\)) and electric potential \((\Delta\phi)\) at normal resting membrane potential for potassium and sodium ions. Arrows indicate the magnitude of the potential and direction of potential gradient from high to low.
For sodium ions the chemical potential and electrical potential differences are both negative at Vm = -70 mV. As a consequence, there is a much larger electrochemical gradient for sodium ions. Sodium ions will move into the cell down their electrochemical gradient.
At a membrane potential of ‑70 mV the potassium ions are much closer to equilibrium than the sodium ions. The membrane potential at which each ion is at equilibrium is known as the equilibrium potential (described in the next section).