Chemical Potential

The starting point for thermodynamic modelling of solute transport across the cell membrane is the proverbial circular cell (Figure 1). There are two-compartments, each filled with an aqueous solution containing solute A. In this example the concentration of solute A is higher outside the cell than inside. The membrane is permeable to solute A.

Figure 1 Model cell. The intracellular and extracellular fluid is an aqueous solution containing only solute A. The two compartments are separated by a membrane that is permeable to solute A.

The movement of solute A either into or out of the cell across the membrane can be formalized as a reversible chemical reaction.

\[A_{\text{out}} \rightleftharpoons A_{\text{in}}\]

Thermodynamical analysis of this system begins by determining the chemical potential, \(\mu\), of the solute in each of the two compartments. The chemical potential of solute A outside and inside the cell is given by,

\[\mu_{A\left( \text{out} \right)} = \mu_{A}^{\circ} + \text{RT\ ln}\left\lbrack A \right\rbrack_{\text{out}}\]

\[\mu_{A\left( \text{in} \right)} = \mu_{A}^{\circ} + \text{RT\ ln}\left\lbrack A \right\rbrack_{\text{in}}\]

where, \(\mu_{A(x)}\) is the chemical potential in compartment \(x\), \(\mu_{A}^{\circ}\) is the standard chemical potential for solute A, R is the gas constant, and T is the absolute temperature (310.15°K at 37°C). Temperature and pressure are constant across the system.

The chemical potential of solute A outside the cell is different to the potential inside the cell because of the difference in solute concentration. The chemical potential is proportional to the log of the solute concentration. The potential increases monotonically with increasing solute concentration (Figure 2).

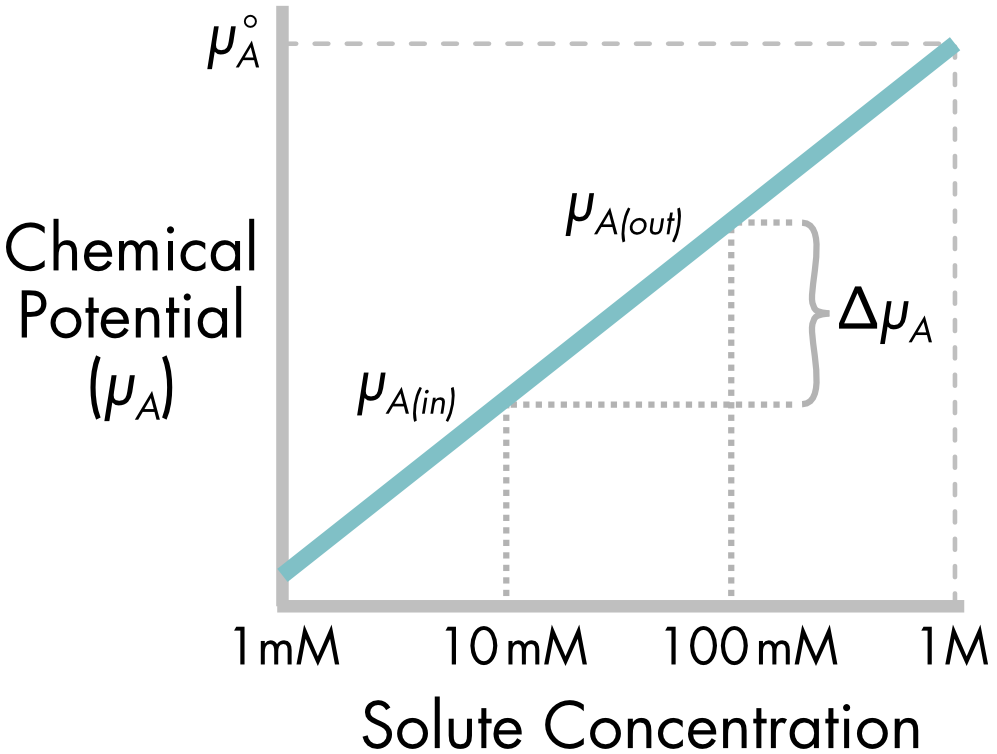
Figure 2 The chemical potential of solute A, \(\mu_{A}\), increases with increasing solute concentration. The chemical potential at 100 mM concentration is greater than at 10 mM and the difference in chemical potential, \({\Delta\mu}_{A}\), is a function of the difference in concentration. The standard chemical potential, \(\mu_{A}^{\circ}\), is calculated at a solute concentration of 1M. Note: solute concentration is plotted on a log scale.

The difference in chemical potential for solute A (\({\Delta\mu}_{A}\)) between the outside and inside of the cell is given by,

\[\begin{aligned}{\Delta\mu}_{A} &= \mu_{A(\text{in})} - \mu_{A(\text{out})}\\\\[-2ex] &= \mu_{A}^{\circ} - \mu_{A}^{\circ} + \text{RT}\text{ ln}\left\lbrack A \right\rbrack_{\text{in}} - \text{RT ln}\left\lbrack A \right\rbrack_{\text{out}}\end{aligned}\]

Conditions inside and outside the cell are identical so the standard chemical potentials for the solute are equal in both compartments. They cancel to give,

\[\Delta\mu_{A} = \text{RT}\ln\frac{\left\lbrack A \right\rbrack_{\text{in}}}{\left\lbrack A \right\rbrack_{\text{out}}}\]

Numerical Example

For the cell shown in Figure 2, if the concentration of solute A outside is 100 mM and the concentration inside is 10 mM, and the temperature is 37 ºC, then the chemical potential difference (∆μ_A) for solute A is given by,

\[\begin{aligned}\Delta\mu_{A} &= \text{RT}\ln\left( 10\text{/}100 \right)\\\\[-2ex] &= 8.31447 \times 310.15 \times - 2.3026\\\\[-2ex] &= - 5.9\,\,\text{kJ}\text{⋅}\text{mo}\text{l}^{\text{-1}}\end{aligned}\]

The chemical potential difference is negative, and the solute will diffuse from out to in because there is a lower chemical potential inside the cell.

The chemical potential allows us to quantify and compare the driving forces that govern the movement of solutes across the membrane.